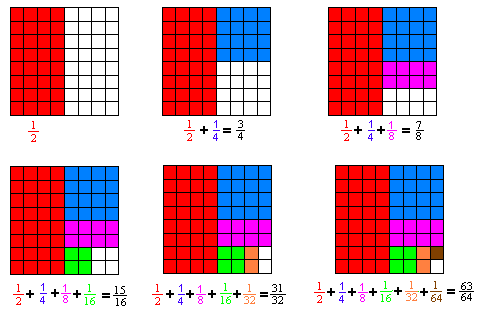
1 2 1 4 1 8 Pattern

There are many different expressions that can be shown to be equivalent to the problem such as the form.

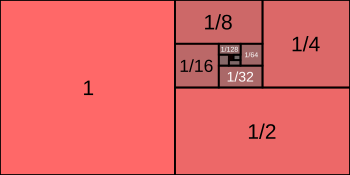
1 2 1 4 1 8 pattern. 1 2 1 4 1 8 7 8. As you can see the half of 1 is 1 2 the half of 1 2 is 1 4 and so on. As a geometric series it is characterized by its first term 1 and its common ratio 2. 1 16 1 2 1 32.

The distance to 1 is 1 8. Sum n 0 i 1 2 n in your question i 4 and you are asking for the value at i 5. How do you think about the answers. 1 32 seems most likely.

1 1 2 1 4 1 8 1 16 1 32 1 64. 2 1 2 2 2 3. The pattern is divide by half like 1 1 2 1 4 1 8 1 16 1 32 etc. In mathematics the infinite series 1 2 1 4 1 8 1 16 is an elementary example of a geometric series that converges absolutely.

Notice that the denominator of each fraction in the sum is twice the denominator that comes before it. What is the next number in the following pattern 1 1 2 1 4 1 8 a. None of these sums will ever be 1 because the next number added is only half of the distance to 1. Dalam matematika deret tak hingga 1 2 1 4 1 8 1 16 adalah contoh dasar dari deret geometri yang konvergen absolut.

In mathematics 1 2 4 8 is the infinite series whose terms are the successive powers of two with alternating signs. The next number you re adding is less than 1 4. The next number you re adding is less than 1 8. This appears to be the geometric series 1 2 n starting at n 0.

If you continue adding on fractions according to this pattern when will you reach a sum of 2. 3 challenging mathematical riddles. 1 2 5 1 32 or alternatively by following the pattern from your already given series values. The distance to 1 is 1 4.

You can sign in to vote the answer. Look at the following sum. You can put this solution on your website. As a series of real numbers it diverges so in the usual sense it has no sum in a much broader sense the series is associated with another value besides.

Answer by jennifertutors 83 show source. 1 2 1 4 3 4.