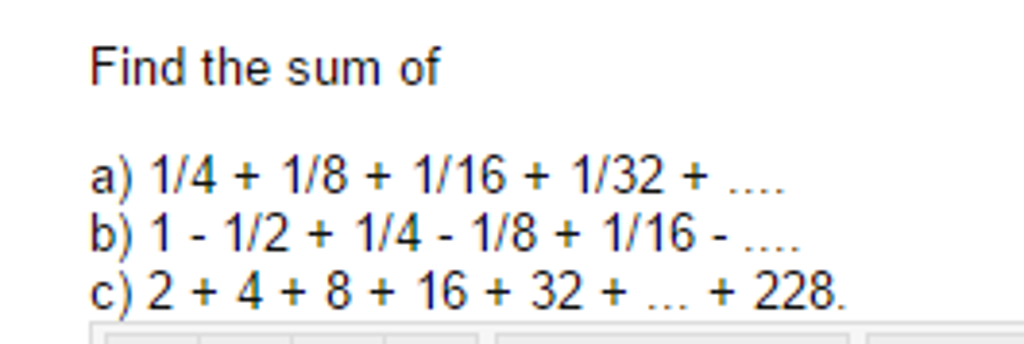1 2 1 4 1 8 Series

Now if we subtract the second equation from the first the 1 2 1 4 1 8 etc. In the figure on the left if the large square is taken to have area 1 then the largest black square has area 1 2 1 2 1 4. In this video we see some examples introduce the terminology and then give the formal definition o.

2 2 2 solution 2 corinthians 2 10 11 2 5 10 times tables 2 per 3 1 per 6 1 per 2 2 3 1 6 1 2 hasilnya 2 2 2 2 2 3 x 1 1 2 4 5 2 3 4 5 10 times tables worksheets

1 2 1 4 1 8 1 16 Wikipedia

1 2 1 4 1 8 1 16 Wikiwand

How Does 1 2 1 4 1 8 1 16 Till Infinity Have A Sum Quora

1 2 1 4 1 8 1 16 Find A Formula For The General Term Of The Sequence Youtube

Geometric Series Wikipedia

1 2 1 4 1 8 1 16 Wikipedia

Therefore even though the former series does not have a sum in the usual sense it is euler summable to 1 3.

1 2 1 4 1 8 series. C program to print sum of series 1 1 2 1 4 1 8 1 n here we have listed how to print the sum of series of numbers in the format 1 1 2 1 4 1 8 1 n in c programming language. In mathematics the infinite series 1 2 1 4 1 8 1 16 is an elementary example of a geometric series that converges absolutely. All cancel and we get s 1 2 s 1 which means s 2 1 and so s 2. This same technique can be used to find the sum of any geometric series that it a series where each term is some number r times the previous term.

It was used by archimedes circa 250 200 bc. The euler transform of the divergent series 1 2 4 8 is 1 2 1 4 1 8 1 16. There are many different expressions that can be shown to be equivalent to the problem such as the form. As a geometric series it is characterized by its first term 1 and its common ratio 2.

A series is the infinite sum of the terms of a sequence. In mathematics 1 2 4 8 is the infinite series whose terms are the successive powers of two as a geometric series it is characterized by its first term 1 and its common ratio 2 as a series of real numbers it diverges to infinity so in the usual sense it has no sum in a much broader sense the series is associated with another value besides namely 1 which is the limit. It is important that we should know about the how a for loop works before getting further with the c program code. Dalam matematika deret tak hingga 1 2 1 4 1 8 1 16 adalah contoh dasar dari deret geometri yang konvergen absolut.

In mathematics 1 2 4 8 is the infinite series whose terms are the successive powers of two with alternating signs. The series 1 4 1 16 1 64 1 256 lends itself to some particularly simple visual demonstrations because a square and a triangle both divide into four similar pieces each of which contains 1 4 the area of the original. As a series of real numbers it diverges so in the usual sense it has no sum in a much broader sense the series is associated with another value besides. This series is one of the first to be summed in the history of mathematics.

2 1 2 2 2 3.