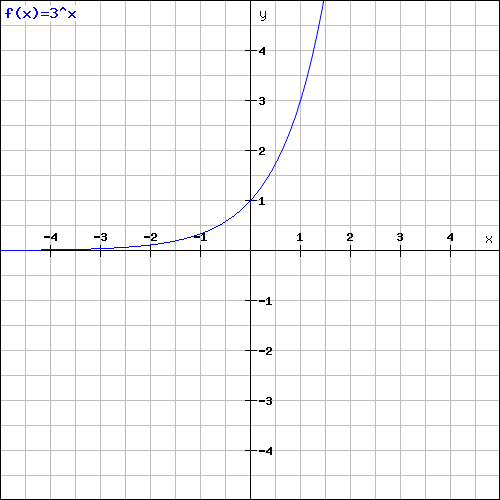
Grafik Fungsi Eksponen F X 3x 1

Tentukan fungsi eksponensial f x a x yang grafiknya diberikan oleh gambar 4 a dan 4 b berikut.

Grafik fungsi eksponen f x 3x 1. Pembahasan pada gambar 4 a kita dapat melihat bahwa f 2 a 25 sehingga kita mendapatkan a 5. F x g x genap sama artinya dengan f x dan g x keduanya genap atau. Apabila a dan a 1 x r maka f x ax kemudian disebut sebagai fungsi eksponen.

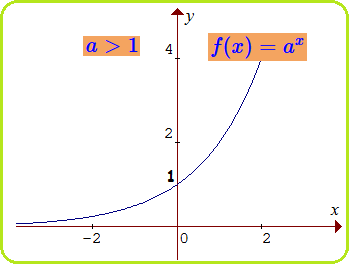
A 0 dan a 1 mempunyai beberapa sifat sifat sebagai berikut. Mengidentifikasi grafik fungsi eksponensial. Fungsi logaritma adalah suatu fungsi invers balikan dari fungsi eksponen. Grafik memotong sumbu y di y 1 dan monoton naik.

Pada pembahasan ini kita akan mempelajari fungsi eksponensial. Perhatikan bahwa fungsi ini naik bertambah dengan sangat cepat. Fungsi eksponen ialah pemetaan bilangan real x ke bilangan ax dengan a 0 dan a 1. Untuk grafiknya adalah grafik monoton turun.

H x f x g x 1 jika h x 1 maka f x dan g x tidak juuga memberikan syarat apapun sebab satu berpangkat sembarang itu bilangan terdefinisi dan hasilnya satu. Berikut disajikan sejumlah soal dan pembahasan terkait fungsi eksponen pangkat yang dipelajari saat kelas x pada mata pelajaran matematika peminatan. Fungsi eksponen adalah fungsi yang variabel bebasnya berupa pangkat dari suatu konstanta dalam persamaan fungsi tersebut. Grafik fungsi eksponen f x a x dapat dilihat dari nilai a yaitu.

Clubsuit untuk nilai a 1. Baca juga artikel yang mungkin berhubungan. Soal juga dapat diunduh dalam format pdf dengan mengklik tautan berikut. Grafik fungsi eksponen tidak memiliki titik potong pada sumbu x dan tidak memiliki nilai ekstrim.

Bila fungsi eksponen dinyatakan dengan f x a x a 0 a 1 maka invers dari f x0 ditulis dengan f 1 x a log x atau f x a log x a 0 a 1. Fungsi eksponensial f dengan bilangan pokok a adalah fungsi yang memetakan setiap bilangan real x ke 𝑎𝑥 dengan 𝑎 0 dan 𝑎 1 dan ditulis sebagai. Fungsi eksponen dan grafiknya. Apabila terdapat bilangan real x maka fungsi eksponen merupakan fungsi yang memetakan bilangan x ke ax dengan syarat a 0 dan a 1 atau dapat dituliskan f x ax.

Fungsi eksponen y f x ax. Jika kita bandingkan fungsi ini dengan fungsi g x x yang menghasilkan g 30 900 kita dapat melihat bahwa jika variabel fungsi berada dalam eksponen maka perubahan kecil pada variabel akan. Jika h x 1 maka f x g x haruslah genap sebab 1 berpangkat ganjil hasilnya bukan satu. Download pdf 340 kb.

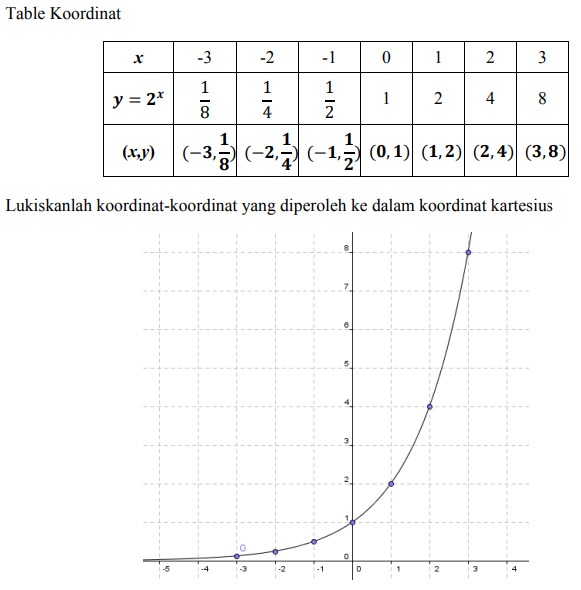
Gambar grafik yang disajikan di dalam postingan ini merupakan produk dari penggunaan aplikasi geogebra. Misalnya merupakan fungsi eksponensial yang memiliki basis 2.